Basic Projectile Kinematics

La parole est un projectile qui tue à distance.

— Adolphe d’Houdetot, Dix épines pour une fleur.

It is time to apply the independence of vertical and horizontal motion to strengthen the power of our military! It is time to launch our first projectiles.

Let be a force. As in the previous tutorials, by abuse of language, we will write , if it is clear, from the context, that we are only interested in the magnitude of the force, and not in its direction or sens.

Basic Equations

A projectile is an object that is launched into motion and then allowed to follow a path determined solely by the influence of gravity. Air resistance and the Earth’s rotation are ignored for the moment.

To simulate projectile motion, the equations of motion of the previous chapter can be used. Since gravity only adds negative vertical acceleration, the acceleration vector can be set to , where stands for the acceleration caused by gravitation: on Earth, the acceleration of gravity is averaged to be . The equations of motion thus look as follows:

Launch Angle

To simplify the computations, the launch site of the projectile is always set to the centre of the coordinate system. The figure below shows a projectile being launched with an initial velocity 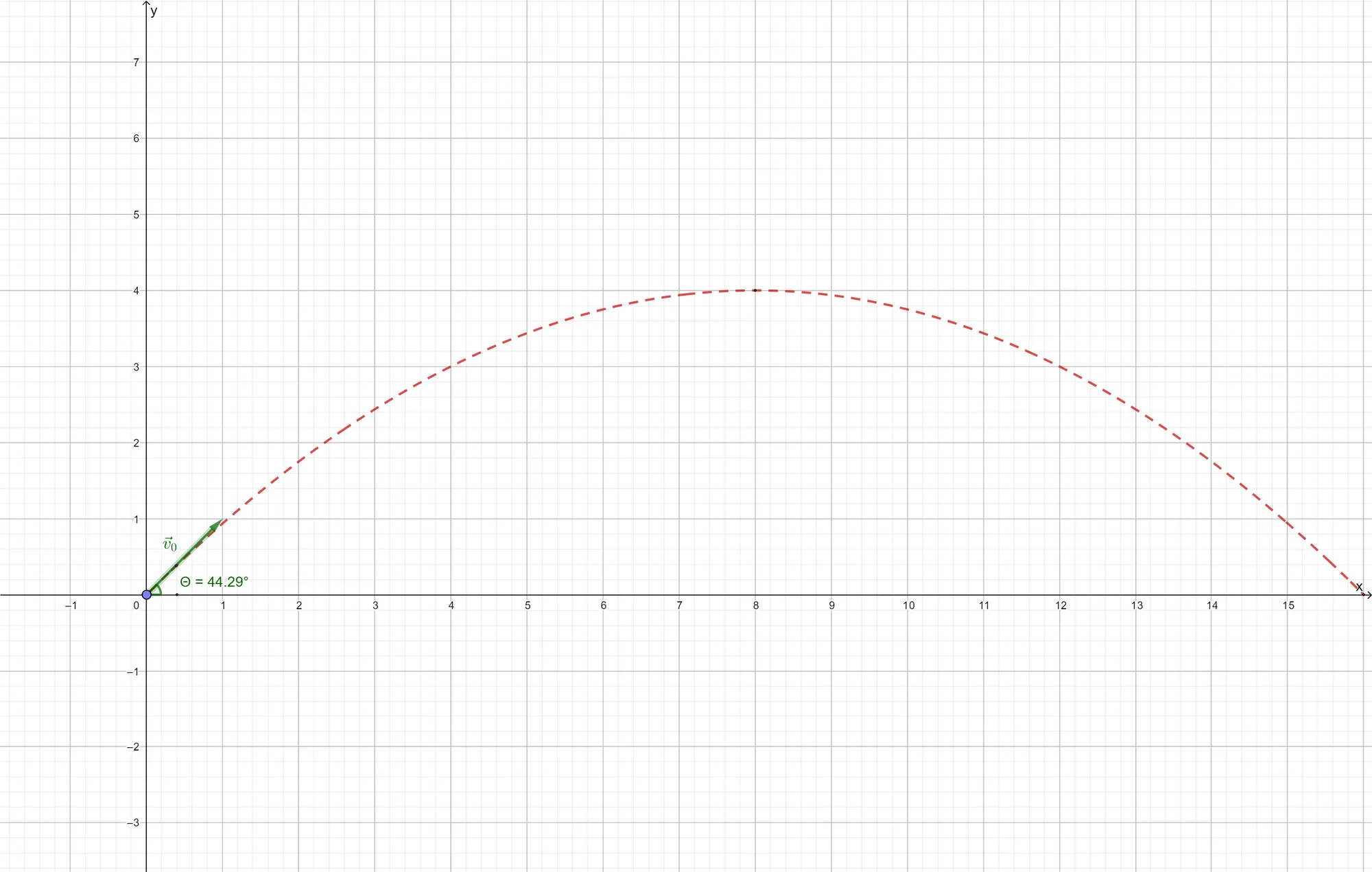and at an angle . ‌

Since the projectile starts at the origin of the coordinate system, its initial position is and . The first task is to find the and coordinates of the initial velocity vector, which can be done using trigonometric functions:where is the launch speed of the projectile (c.f. figure below).

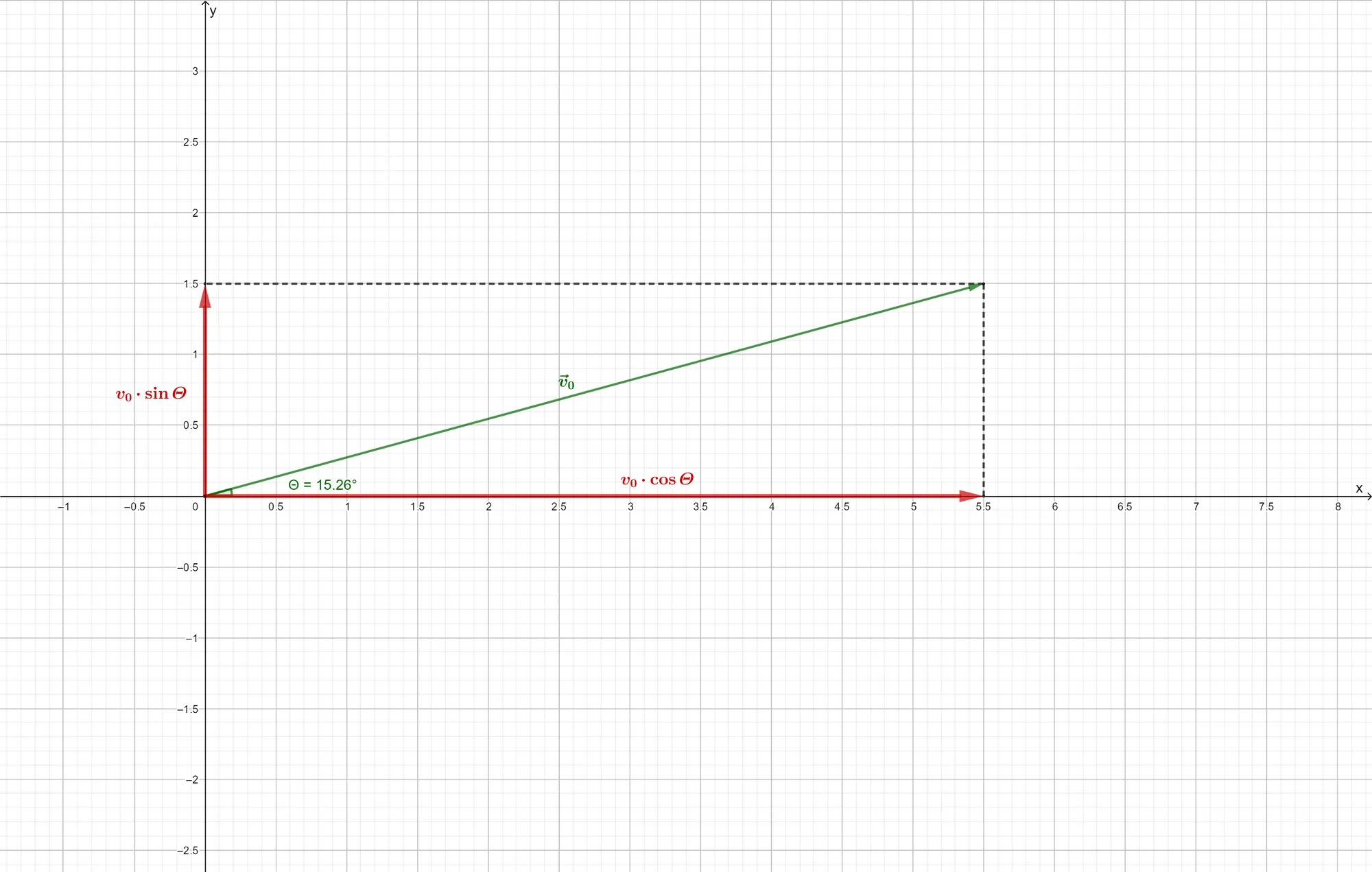
Decomposition of a vector

The launch angle of the projectile is and its initial speed is at , thus the initial horizontal velocity is , and the initial vertical velocity .

Using this new idea, the equations of motion for a projectile launched with an initial speed and at an angle , transform into the following:

where is the launch site of the projectile.

We will only discuss frictional forces in later tutorials, but just as an idea, to add, for example, a small wind force, slowing down a bullet, a small negative vertical acceleration could be used:

Key Characteristics

To complete this rather short tutorial, some key characteristics of projectile movement are briefly explained.

Height, Range and Time

The total time for which the projectile remains in the air is called the time of flight. The time it takes for a projectile, launched from the centre of the coordinate system, to hit the ground, can be calculated by solving the equation . The solution is .

If the projectile is instead launched from a launch site located at , then the time it takes for the projectile to hit the ground can be calculated by solving the equation . The positive solution of that equation is

which, for , simplifies to the above solution of a launch from the centre of the coordinate system.

The peak , or the maximal height, above its launch site, obtainable by a projectile, can be calculated by observing that the projectile will continue to rise until , that is, until its velocity in the -direction becomes , thus until . The time it takes to reach the peak is , and the actual peak of the projectile is thus .

The range of a projectile is the maximal horizontal distance the projectile travels before it hits the ground. The range can be calculated by plugging in the time it takes the projectile to hit the ground into the equation for the motion in the -axis. The actual solution is

for a projectile launched at an initial height of , thus , for a projectile launched from the centre of the coordinate system.

Note that the range depends inversely on the acceleration of gravity, thus the smaller the gravity, the larger the range; this means that a projectile launched on the Moon, where the acceleration of gravity is about smaller than on Earth, travels about six times as far as it would on our blue planet.

As the range varies with the double of the initial launch angle, the maximal reach can be obtained by using a launch angle of , as Obviously this is only true if there is no air resistance at all. The maximal range is then given by .

Symmetrical Range

When wondering at what range to shoot a projectile, the following symmetry might be handy. Under ideal conditions (no air resistance), the maximal range is obtained by a launch angle of . Now launching a projectile with an angle of , with , obviously, leads to the same range as launching with an angle of .

Angle of Reach

Given a distance , the angle of reach is the angle at which a projectile must be launched in order for its range to achieve the desired distance, given an initial speed . If the projectile was launched from the centre of the coordinate system, then the angle of reach is the solution of the equation: . The two solutions, see above, are and .

Angle to Hit

To hit a target located at a point , when fired from the centre of the coordinate system, with an initial speed of , the projectile must be launched at an angle of

If the roots are imaginary, then the initial speed of the projectile was not fast enough to reach the desired target.

The case where both roots are the same is very intriguing, as it defines the angle that allows for the lowest launch speed. For that to happen, the value under the square root must be zero, thus the solutions to the equation must be found.

Those solutions are and . Using a completely positive solution, the above equation for the angle required to hit the target reduces to . Now let , then a solution to the equation is given by , thus .

In other words, to be able to use the lowest possible launch speed, the launch angle should be chosen as the arctangent of the ratio of the elevation of the target over the distance of the target, plus , which means one half of the angle between the target and the opposite of the vector of the acceleration of gravitation.

Symmetrical Velocity

Note that when a projectile hits the ground, its velocity in the -direction is , which is the opposite of its initial velocity. Under ideal conditions (no air resistance), the speed of the projectile is the same on hit than on launch.

Implementation

Implementing projectile movement can once again be done using the symplectic integrator from the previous chapters.

To facilitate working with projectiles, I created a new class called Projectile:

class Projectile
{
private:
  // key characteristics
  float launchSpeed;            // launch speed in pixels per second
  float launchAngle;            // launch angle in degree
  float gravity;              // acceleration of gravity in pixels per second
  float range;              // range in pixels
  float peak;                // peak in pixels
  float timeOfFleight;          // in seconds

  // update
  mathematics::Vector2F position;      // the current position of the projectile (in pixels)
  mathematics::Vector2F velocity;      // the current velocity of the projectile (in pixels per second)
  mathematics::Vector2F acceleration;    // the current acceleration of the projectile (in pixels per seconds squared)

  // recompute initial velocity and key characteristics
  void computeInitialVelocityAndKeyCharacteristics();

public:
  // constructor
  Projectile(const float launchSpeed, const float launchAngle, const float launchX = 0.0f, const float launchY = 0.0f, const float gravity = 9.81f, const float frictionX = 0.0f);

  // update and farseer
  void update(const double dt);      // updates the position of the projectile - uses semi-implicit Euler integration

  // recalibrate projectile
  void setLaunchAngle(const float angle);
  void reduceLaunchAngle();
  void increaseLaunchAngle();
  void reduceLaunchSpeed();
  void increaseLaunchSpeed();
  void increaseGravity();
  void decreaseGravity();

  // getters
  float getPositionX() const { return position.x; };
  float getPositionY() const { return position.y; };
  float getRange() const { return range; };
  float getVelocityX() const { return velocity.x; };
  float getVelocityY() const { return velocity.y; };
  float getMovementDirection() const;
};

The constructor simply sets the initial values:

Projectile::Projectile(const float launchSpeed, const float launchAngle, const float launchX, const float launchY, const float gravity, const float frictionX) : launchSpeed(launchSpeed), launchAngle(launchAngle), gravity(gravity)
{
  // set starting position
  position.x = launchX;
  position.y = launchY;

  // set initial acceleration
  acceleration.x = -frictionX;
  acceleration.y = this->gravity;

  // compute initial velocity
  computeInitialVelocityAndKeyCharacteristics();
}

The key characteristics are computed as explained above:

// compute initial velocity and key characteristics
void Projectile::computeInitialVelocityAndKeyCharacteristics()
{
  // get launch angle in radians
  float launchAngleRad = ((float)M_PI / 180)*launchAngle;

  // compute starting velocity
  float cosAngle = std::cosf(launchAngleRad);
  float sinAngle = std::sinf(launchAngleRad);
  velocity.x = launchSpeed * cosAngle;
  velocity.y = -launchSpeed * sinAngle;

  // calculate characteristics
  if (position.x == 0 && position.y == 1080)
  {
    // starting position is at the lower left of the screen
    timeOfFleight = (2 * launchSpeed / gravity)*sinAngle;
    range = (launchSpeed*launchSpeed / gravity) * 2 * sinAngle*cosAngle;
  }
  else
  {
    timeOfFleight = (launchSpeed*sinAngle + std::sqrtf(launchSpeed*launchSpeed*sinAngle*sinAngle + 2 * gravity*position.y)) / gravity;
    range = (launchSpeed*launchSpeed*std::sinf(2 * launchAngleRad)) / (2 * gravity) * (1 + std::sqrtf(1 + (2 * gravity*position.y) / (launchSpeed*launchSpeed*sinAngle*sinAngle)));
  }

  peak = (launchSpeed * launchSpeed * sinAngle * sinAngle) / (2 * gravity);
}

To update the position of a projectile, the symplectic Euler integrator is used once again:

// update position
void Projectile::update(const double dt)
{
  // update the position and velocity of the projectile using semi-implicit Euler integration
  Kinematics::semiImplicitEuler(position, velocity, acceleration, dt);
}

To use the class, simply create a projectile and launch it. Here is the code for the rendering function of a little demo I created:

util::Expected<void> PlayState::render(const double farSeer)
{
  // render preview for the current projectile
  dxApp.getGraphicsComponent().get2DComponent().drawEllipse(currentProjectile->getPositionX(), currentProjectile->getPositionY(), 5.0f, 1.2f);
  dxApp.getGraphicsComponent().get2DComponent().drawEllipse(currentProjectile->getRange(), 1080, 5.0f, 5.0f);

  // render projectiles
  for (unsigned int i = 0; i < projectiles.size(); i++)
  {
    // render landing zone
    dxApp.getGraphicsComponent().get2DComponent().fillEllipse(projectiles[i].getRange(), 1080, 5.0f, 5.0f);

    // render projectile
    dxApp.getGraphicsComponent().get2DComponent().setRotationMatrix(projectiles[i].getMovementDirection(), projectiles[i].getPositionX(), projectiles[i].getPositionY());
    dxApp.getGraphicsComponent().get2DComponent().drawEllipse(projectiles[i].getPositionX() + projectiles[i].getVelocityX()*farSeer*dxApp.getPhysicsDeltaTime(), projectiles[i].getPositionY() + projectiles[i].getVelocityY()*farSeer*dxApp.getPhysicsDeltaTime(), 25.0f, 2.5f);
        dxApp.getGraphicsComponent().resetTransformation();
  }

    // print FPS information
  dxApp.getGraphicsComponent().getWriteComponent().printFPS();

  // return success
  return { };
}

Note that in order for the ellipses to point in the direction of movement, a rotation matrix is set using a formula from the previous tutorial on two-dimensional motion:

Furthermore, the far seer is used to guess the position of a projectile, if there is some time left over that could not be processed during the update of the game world. If you can’t recall why exactly we use a far seer in our game loop, reread the following tutorial on the game loop. Basically, to make sure we can simulate our mathematical and physical world with as much precision as possible, a fixed time step is used to do numerical integration, for example, yet sporadically, there is still some unprocessed time left over, and the renderer then makes an educated as to where the projectile should be drawn.

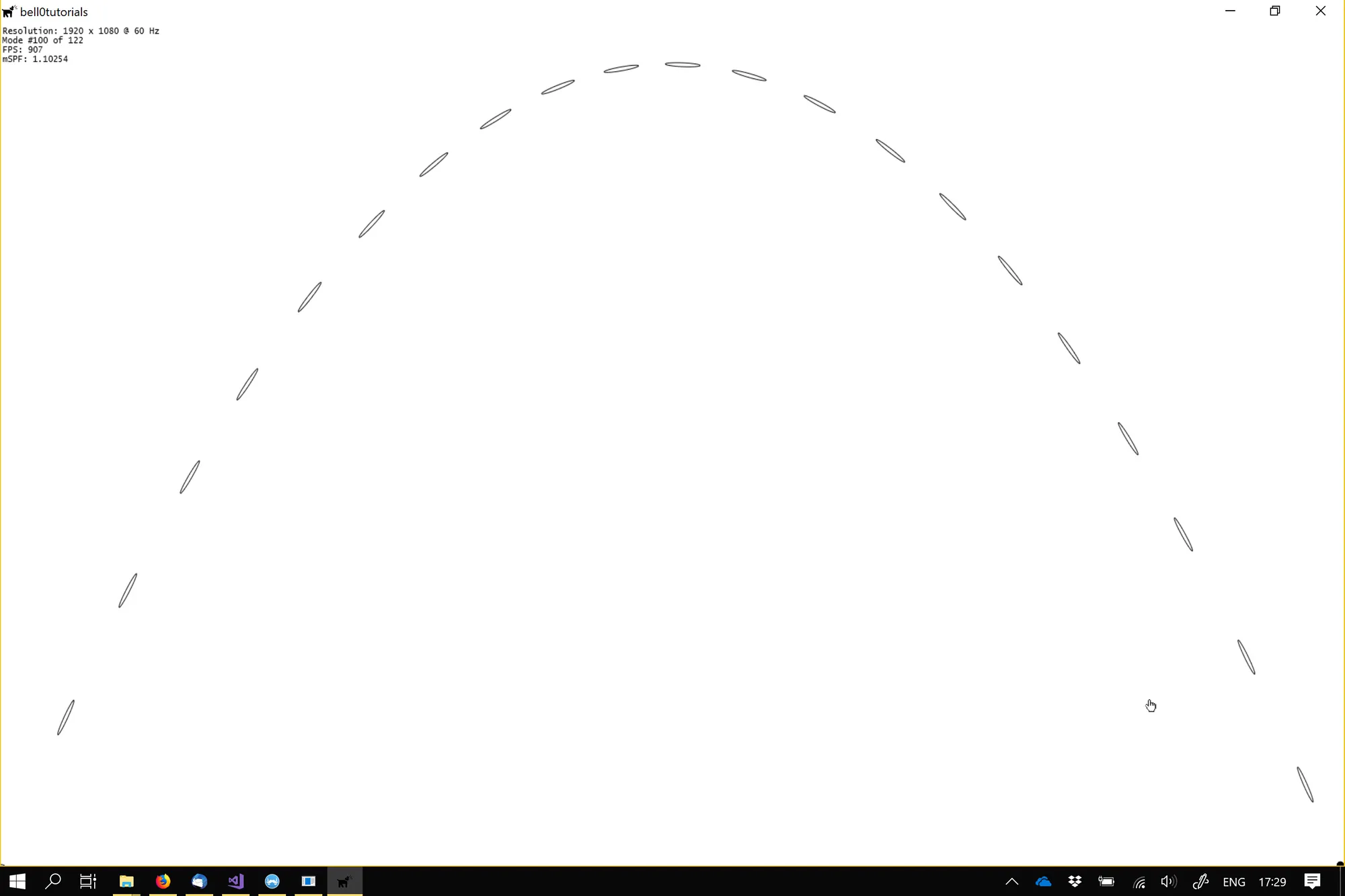
Missile Barrage

The entire source code can be downloaded from here. In the demo, use the arrow keys to change the launch angle (left and right arrow keys) as well as the launch velocity ( up and down arrow keys). The acceleration of gravity can be changed by pressing A or Q.

In the next tutorial, we will learn about Newton’s laws of motion. For now though, enjoy the missile barrage!

References

Geogebra
Physics, by James S. Walker
Tricks of the Windows Programming Gurus, by A. LaMothe
Wikipedia